gongdear

Momentum

momentum即动量，它模拟的是物体运动时的惯性，即更新的时候在一定程度上保留之前更新的方向，同时利用当前batch的梯度微调最终的更新方向。这样一来，可以在一定程度上增加稳定性，从而学习地更快，并且还有一定摆脱局部最优的能力。

具体实现:

需要:学习速率 ϵ, 初始参数 θ, 初始速率v, 动量衰减参数α

每步迭代过程:

从训练集中的随机抽取一批容量为m的样本{x1,…,xm},以及相关的输出yi

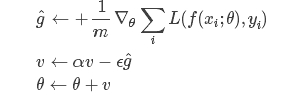
计算梯度和误差,并更新速度v和参数θ:

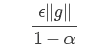
其中参数α表示每回合速率v的衰减程度.如果每次迭代得到的梯度都是g,那么最后得到的v的稳定值为：

也就是说,Momentum最好情况下能够将学习速率加速1/(1−α)倍.一般α的取值有0.5,0.9,0.99这几种，分别表示最大速度2倍，10倍，100倍于SGD的算法。.当然,也可以让α的值随着时间而变化,一开始小点,后来再加大.不过这样一来,又会引进新的参数.

特点:

• 前后梯度方向一致时,能够加速学习
• 前后梯度方向不一致时,能够抑制震荡

Nesterov Momentum

这是对传统momentum方法的一项改进，由Ilya Sutskever(2012 unpublished)在Nesterov工作的启发下提出的。

具体实现:

需要:学习速率 ϵ, 初始参数 θ, 初始速率v, 动量衰减参数α

每步迭代过程:

从训练集中的随机抽取一批容量为m的样本{x1,…,xm},以及相关的输出yi

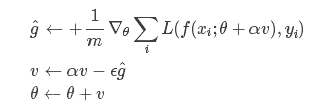
计算梯度和误差,并更新速度v和参数θ:

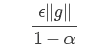
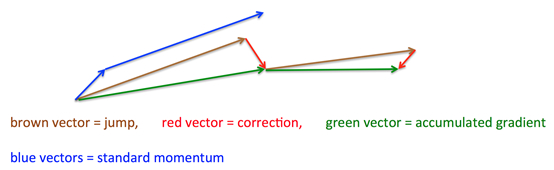
注意在估算梯度g的时候,参数变成了θ+αv而不是之前的θ，与Momentum唯一区别就是，计算梯度的不同，Nesterov先用当前的速度v更新一遍参数，在用更新的临时参数计算梯度。

其基本思路如下图（转自Hinton的coursera公开课lecture 6a）：